# Key concepts
# High-level design diagram
Data processing consists of three phases.
# Phase 1. Parsing and construction of ASTs
Formulas need to be parsed and represented as a
so-called
Abstract Syntax Tree (opens new window)
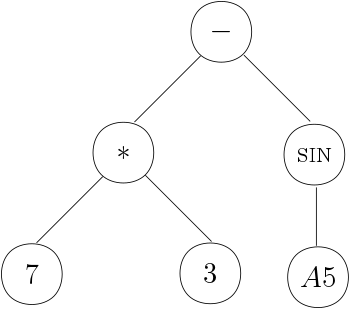
(AST). For example, the AST for 7*3-SIN(A5) will look
similar to this graph:
# Phase 2. Construction of the dependency graph
HyperFormula needs to understand the relationship between cells and
find the right order of processing them. For example, for a sample
formula C1=A1+B1, it needs to process first A1 and B1 and
then C1. Such an order of processing cells - also known as
topological order (opens new window)
exists if and only if there is no cycle in the dependency graph.
There can be many such orders, like so:
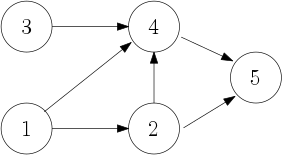
Read more about the dependency graph.
# Phase 3. Evaluation
It is crucial to evaluate cells efficiently. For simple expressions, there is not much room for maneuver, but spreadsheet-like data sets definitely need more attention.

# Grammar
For parsing purposes, the library uses the Chevrotain (opens new window) parser, which turns out to be more efficient than popular Jison (opens new window). The language of acceptable formulas is described with an LL(k) grammar using Chevrotain Domain Specific Language. See details of the grammar in the FormulaParser (opens new window) file.
# Repetitive ASTs
A first natural optimization could concern cells in a spreadsheet which store exactly the same formulas. For such cells, there is no point in constructing and storing two ASTs which would be the same in the end. Instead, HyperFormula can look up the particular formula that has already been parsed and reuse the constructed AST.
A scenario with repeating formulas is somewhat idealized; in practice, most formulas will be distinct. Fortunately, formulas in spreadsheets usually have a defined structure and share some patterns. Neighboring cells often contain similar formulas, especially after filling cells using a fill handle (that little square in the bottom right corner of a visual cell representation). For example:
B2=A2-C2+B1B3=A3-C3+B2B4=A4-C4+B3B5=A5-C5+B4- and so on...
Although the exact ASTs for these formulas are different, they share a common pattern. A very useful approach here is to rewrite a formula using relative addressing of cells.
# Relative addressing
HyperFormula stores the offset to the referenced formula. For example
B2=B5 + C1 can be rewritten as B2=[B+0][2+3] + [B+1][2-1] or in short
B2=[0][+3] + [+1][-1]. Then, the above example with B2,B3, and B4
can be rewritten as B2=B3=B4=[-1][0] - [1][0] + [0][-1]. Now the three
cells have exactly the same formulas.
By using relative addressing HyperFormula unifies formulas from many cells. Thanks to that, there is no need to parse them all over again. Also, with this approach, the engine doesn't lose any information because by knowing the absolute address of a cell and its formula with relative addresses, it can easily retrieve the absolute addresses and compute the result.
# Laziness of CRUD operations
After each CRUD operation, like adding a row or column or moving cells, references inside formulas may need to be changed. For example, after adding a row, we need to shift all references in the formulas below like so:

In more complex sheets this can lead to similar transformations in many formulas at once. On the other hand, such operations do not require an immediate transformation of all the affected formulas.
Instead of transforming all of them at once, HyperFormula remembers the history of the operations and postpones the transformations until the formula needs to be displayed or recalculated.
